I just spent half a day trying to wrap my brain around how to detect cycles within linked lists, as well as how to find the first node of the cycle. After perusing all the Stack Overflow and Wikipedia entries, I had a pretty good mechanical understanding of the most elegant solution, which is known as Floyd’s Cycle-Finding Algorithm, or more informally, the tortoise and the hare algorithm.

The problem with my mechanical understanding was that it’s a classic case of surface-level learning, the kind of sloppy, rote-memorization cramming that somehow powered me through UCI to a 3.2 GPA but left me utterly uninterested and disengaged from my craft. I’d perform well if an interviewer asked me that question tomorrow, but I’d feel like a charlatan if I only parroted an answer back at him. Just because I flipped through some old tome and found an incantation that allowed me to cast a black magic wizard spell doesn’t make me Harry Potter.

I wanted an intuitive understanding of the solution. If I have that, I will carry it for the rest of my life.

In the name of that pursuit, I sat down and turned that problem over and over through my head until I found an elegant way to visualize and understand the reason behind the math. Since it’s an approach I wish I’d thought of six hours ago, I want to share it.

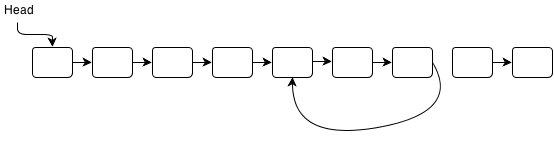
First off, let’s assume everyone knows what a linked list is. I’m talking about your standard, garden-variety singly linked list: it has a head pointer but no tail pointer, made up of nodes that contain a pointer to the next node in the list (except for the last node, which points to null).

A linked list with a cycle in it has one or more nodes that point to a previous node in the list. If you traverse the node starting from the head, you’ll get caught in the cycle loop.

Did you ever play Super Mario Bros. 1? On the Level 8 and 9 dungeons, if you didn’t go the right path, you would cycle backwards until you did. It’s sort of like that.

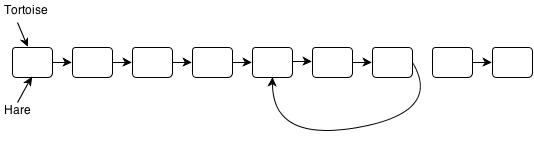
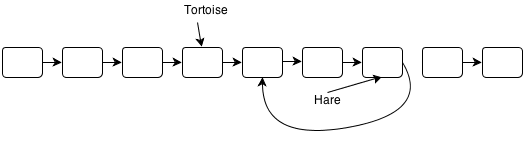
The Floyd Cycle Detection Algorithm works by using two pointers, one slow and one fast. We’ll call them the tortoise and the hare, respectively. They start at the first node.

The hare travels 2 nodes per move, and the tortoise travels 1 node per move.

And so on. If the hare pointer meets the tortoise pointer, you’ve got yourself a cycle:

To visualize why this works, let’s go back to our Mario analogy. Imagine you could play a co-op two-player mode of those cycle-containing dungeons. If Luigi always moved slower than Mario, and Mario keeps hitting the cycle part of the dungeon, Mario will at some point pass Luigi.

But why do we choose to go 2 nodes per move? Couldn’t you go 3 nodes per move? Well, yes, you could, but it’s not important how fast the hare goes. The hare could go light speed for all we care, but it can only pass the tortoise once the tortoise reaches the cycle.

There are some interesting properties about this algorithm:

• The hare is always twice as many steps ahead of the tortoise (if an interviewer asks you how to find the middle of a linked list, have the hare run off the end of your list and the tortoise will be at exactly the middle)
• The hare can never “skip” over the tortoise without them first sharing the same node. It seems like it might because it moves in chunks of two, but remember that for each step, the hare only gains one node on the tortoise.

Now that we can detect cycles, the next step is figuring out where the cycle starts and how to fix the cycle. This is where it gets tricky.

All of the Stack Overflow answers talk about the tortoise being Xi, the hare being X2i, and lambda (the length of the cycle) and mu (the number of steps to get to the cycle).

Let’s toss that all aside and agree upon this: the hare has always taken twice as many steps as the tortoise, right? Right.

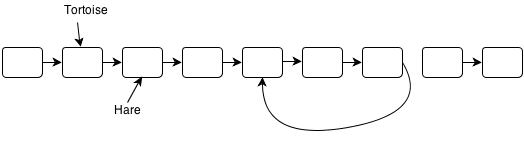
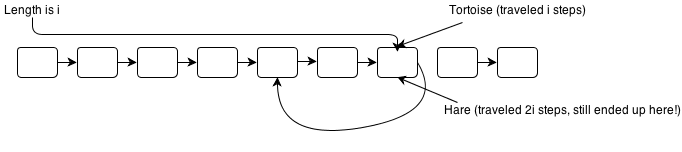
So the tortoise and the hare meet at a particular node for the first time. The tortoise has entered the cycle but hasn’t done a full loop. The hare, depending on the size of the list and the cycle, may have done the loop only once, or it could have done the loop a million times. However, no matter how many times the poor hare has been spun through the cycle, we can guarantee that it has traveled twice as many steps as the tortoise has.

Again, that’s very important. It means that at that meeting point node, if the tortoise has taken i steps, and if the tortoise takes another i steps (i + i = 2i), it will end up at that same node. If it’s a big loop, it’ll only have to loop once, but if it’s a tight loop, it might go through it a lot of times, just like the hare had to do. But no matter what, we can guarantee that it’ll end up on the meeting node after i steps.

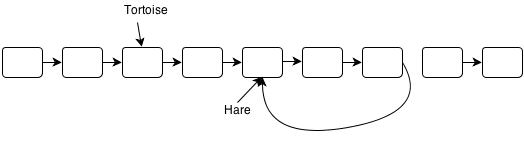
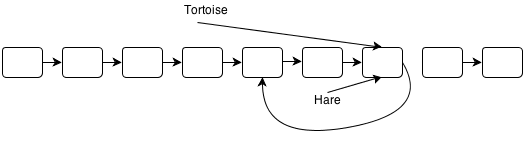
So here’s the heart and soul of Floyd’s Cycle Detection Algorithm: if we cloned the tortoise and placed one at the head of the list and one at the meeting point node, if we had them take i steps, we would guarantee that they would reach the meeting point node at the same time. Why? Because the cloned tortoise starts at position i and takes i steps, which makes a total distance of 2i.

But think about it: they wouldn’t just meet at the meeting point node, they would meet for all of the nodes at the beginning of the cycle until they reached the meeting point node. In fact, it means that the very first node that they meet is the very first node of the cycle.

Once we know the first node of the cycle, fixing the cycle is trivial: plop down a pointer to this first node, and use another pointer to traverse the rest of the cycle until you reach the node who points at the first node.